Modified: August 02 2024

---

The Role of Algorithms in Computing

1.1 Algorithms

Algorithm: Any well defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output in a finite amount of time.

We often say algorithms help us solve computational problems.

We can define a sorting algorithm like so:

Input: A sequence of n numbers, {a_1, a_2, ... a_n}

Output: A permutation (reordering) {a_1,a_2,...a_n} of the input sequence such that a_1 <= a_2 <= ... <= an

If given (7, 3, 12, 1, 5), the correct sorting algorithm, would return (1, 3, 5, 7, 12).

The input sequence is called an instance of the sorting problem.

The instance of a problem is an input sequence needed to compute a solution to said problem.

Sorting is a fundamental concept in programming, considering how many times one is used as an intermediate step.

To that affect, different sorting algorithms are good at accomplishing different things.

We consider an algorithm for a computational problem as correct, if for every instance, it halts - or stops in a finite time and outputs the correct solution to the problem instance.

What kinds of problems are solved by algorithms?

• The Human Genome Project, identifying the unique 30,000 Human DNA genes, uses complex Algorithms, Dynamic Programming among them.
• The internet, using algorithms to determine the best route to send data, and search engines find pages on most relevant information.
• Electronic Commerce allows for exchange of goods and services; public-key cryptography and digital signature are based on numerical algorithms & number theory.

We can look at specific problems:

• Shortest route to destination (Chapter 22)
• Doctors using clustering algorithms for tumors (Chapter 33)
• Compression (Chapter 15)

Problems that can be solved with Algorithms have two common characteristics:

1. They have lots of candidate solutions, most which don’t solve the problem, and finding the best is hard.
2. They have practical applications

7/23/24

Some problems are so complex, no algorithm can solve them in an appropriate amount of time. We call these types of problems NP-Complete problems (see Chapter 34).

1. No one knows if efficient algorithms exist for NP-complete problems
2. If a solution exists for one, a solution exists for all of them
3. No NP-complete problem is the same, but they are similar.

NP-complete problems appear often in everyday solutions.

We might have access to computers with multiple cores, which allows for “Task-Parallelism” (see Chapter 26).

Algorithms that receive input over time, rather than having input present at the start, are called online algorithms (see Chapter 27).

Exercises 1.1

1. Describe your own real-world example that requires sorting. Describe one that requires finding the shortest distance between two points.

A quick example: organizing socks (low-cut vs. high-cut). Distance: when j-walking

2. Other than speed, what other measures of efficiency might you need to consider in a real-world setting?

Legibility: can the algorithm produce output that is easily understandable? Is the algorithm itself readable?

3. Select a data structure that you have seen, and discuss it’s strengths and limitations.

A USB Stick:

• Pros: Able to travel easily, holds most files
• Cons: Not large usually (storage wise), easy to wash/lose

4. How are the shortest-path and traveling salesperson problems given above similar? How are they different?

Similarities: Both deal with distance, and need to know/search for their paths before traveling.

Differences: Shortest-path deals with A - B, while traveling-salesperson has to account for n number of stops, and compare each iteration to find the most efficient.

5. Suggest a real-world problem in which only the best solution will do. Then, come up with one in which “approximately” the best solution is good enough.

I would say something as inconsequential as perfect or near-perfect, it would come down to a question of scope and overall consequences. Let’s take for example, fixing the subway stations here in NYC. The route in which stations are fixed, or sorted, should be intentional. This would facilitate a best-case scenario decision only. However, if there is no best case, where everyone is inconvenienced regardless of the route, the near best would be acceptable.

6. Suggest a real-world problem in which sometimes the entire input is available before you need to solve a problem, but other times the input is not entirely available in advance and arrives over time.

Shipping statistics is the first that comes to mind. We know when we place an order, where the order is going, and an approximation that is usually accurate. This isn’t always the case however. Unexpected weather conditions always throw off shipping dates.

1.2 Algorithms as a technology

If computers were infinitely fast, any method that’s correct for solving a problem would do.

You should choose algorithms that use the resources of time and space efficiently; both are precious.

Efficiency

Let’s consider two sorting methods:

1. Insertion Sort: takes C_1n^2 to sort n items, where C_1 is a constant, but we can just say it takes n^2
2. Merge Sort: takes C_2n lg n, where lgn stands for log_2 n and C_2 is another constant

Insertion sort typically has a smaller constant factor than merge sort, so that C_1 < C_2. However, constant factors have far less of an impact on running time than the dependency of the input size.

We can take the two above and explain their run times as so:

• Insertion: C_1*n*n
• Merge: C_2*n*lgn

For larger numbers, lgn will always return smaller than n.

When n=1000, lgn = 10. When n=1000000, lgn = 20.

Basically, we should be using insertion sort for smaller input sizes, and merge for larger.

Algorithms should be understood as a technology. Even though technology has advanced to abstraction being the primary objective of most software, everything regardless uses algorithms in some way.

Having a solid base of algorithmic knowledge and technique is one characteristic of a good programmer.

Exercises 1.2

1. Give an example of an application that requires algorithmic content at the application level, and discuss the function of the algorithms involved.

Instagram is a really easy answer. The feed is literally called “the algorithm”. It’s based off many different factors. Said algorithm dictates your engagement to a certain extent.

2. Suppose that for inputs of size n on a particular computer, insertion sort runs in 8n^2 steps and merge sort runs in 64nlogn steps. For which values of n does insertion sort beat merge sort?

We can start by using an example of just 10 instructions, then incrementing up by increasing the exponent by 1 We’ll be dividing by 10^7, our virtual computer that can perform that many tasks per minute. Our answer will be returned in seconds.

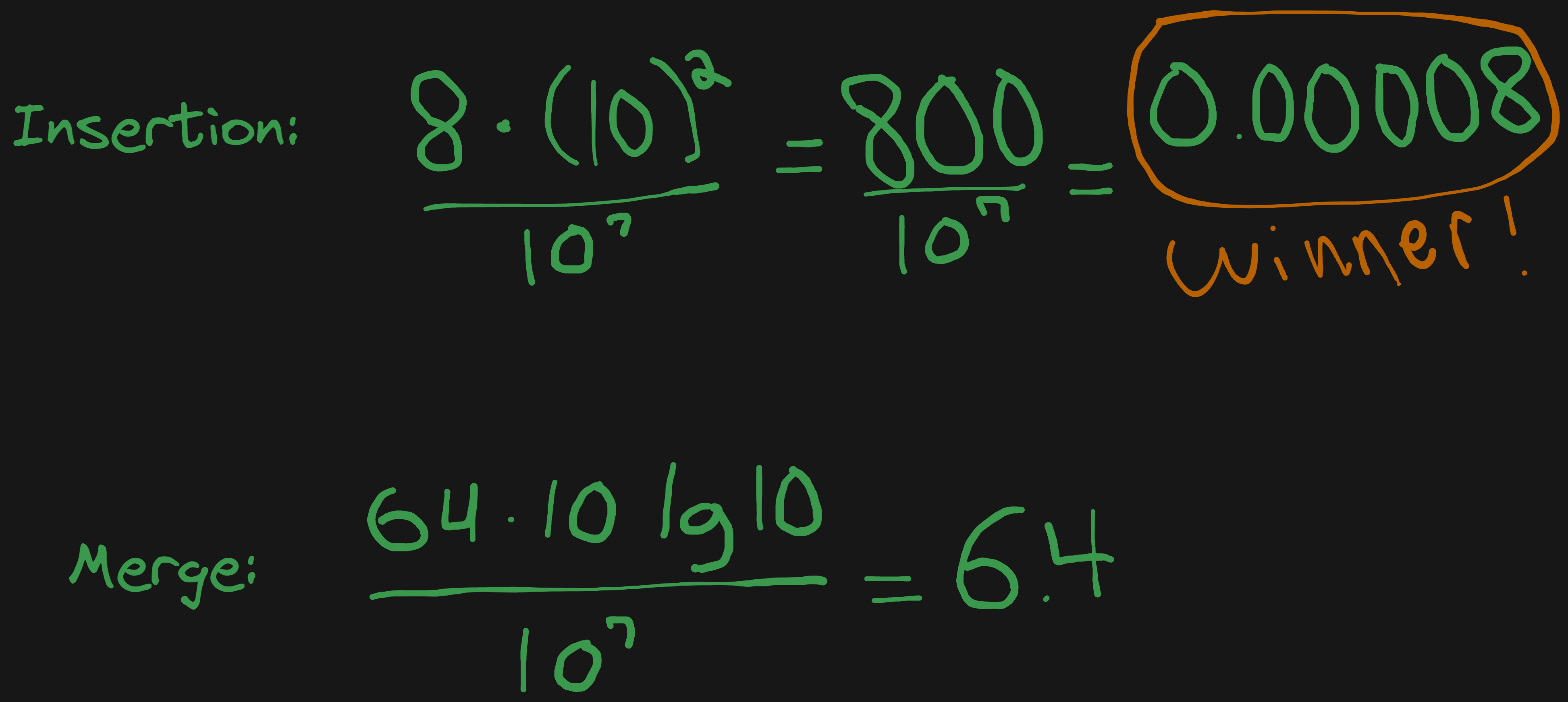
Insertion sort is faster, so we keep going. Let’s go up to the next interval, 10^2 instructions.

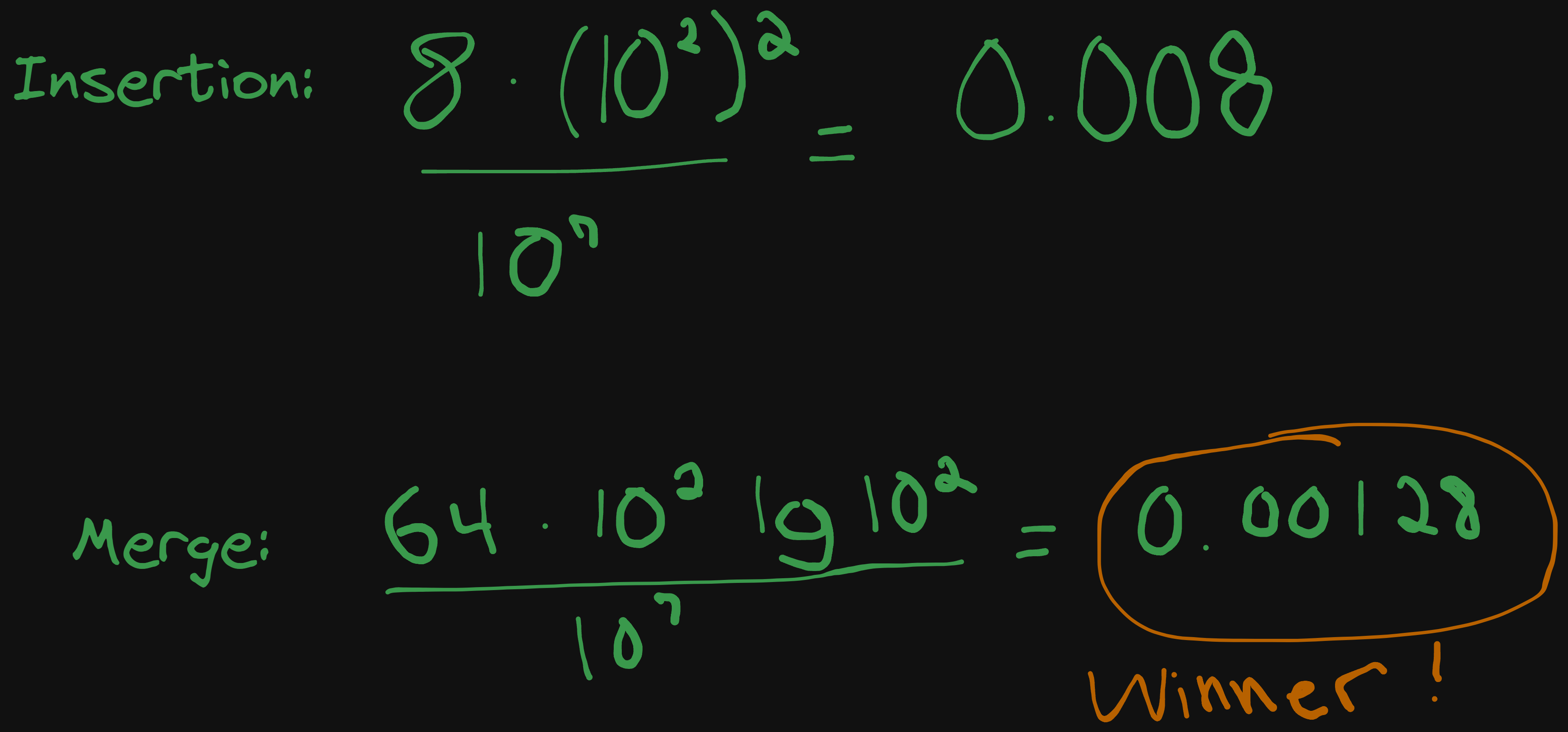
So, we see that somewhere between 10 and 100 commands, merge sort begins to beat out insertion. I also tried 50, which Merge sort still beat. I ended up testing until I found out the exact one which is a bit boring so the answer is 27.

3. What is the smallest value of n such that an algorithm whose running time is 100n^2 runs faster than an algorithm whose running time is 2^n on the same machine?

We’ll be using the same machine time (10^7) and starting at 10 instructions, and incrementing up.

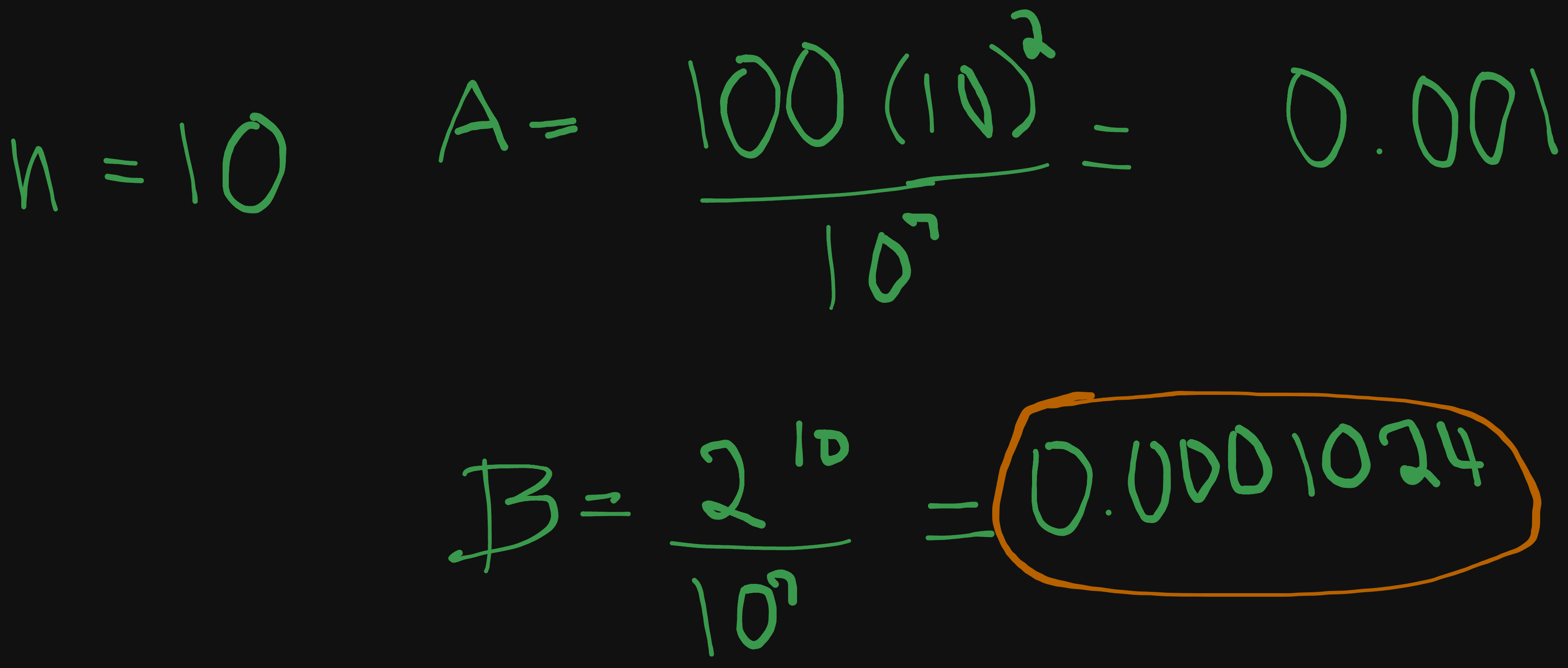
B is faster, but not by so much, so let’s only increment up a little, to lets say 15.

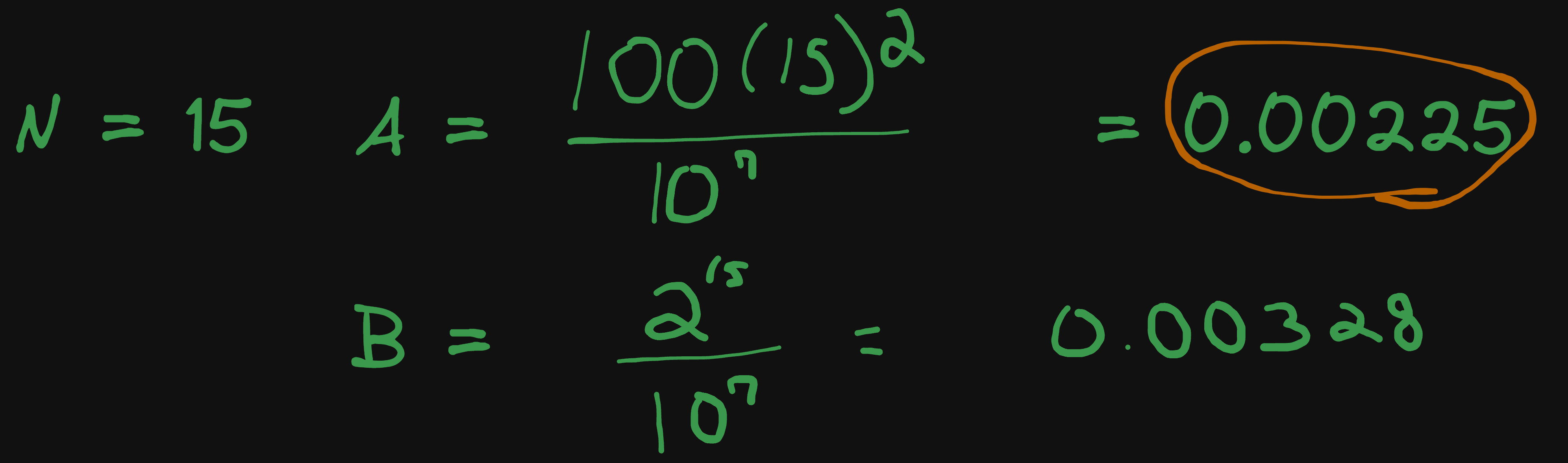
A is faster! But is this the minimum value? Let’s go down one to make sure.

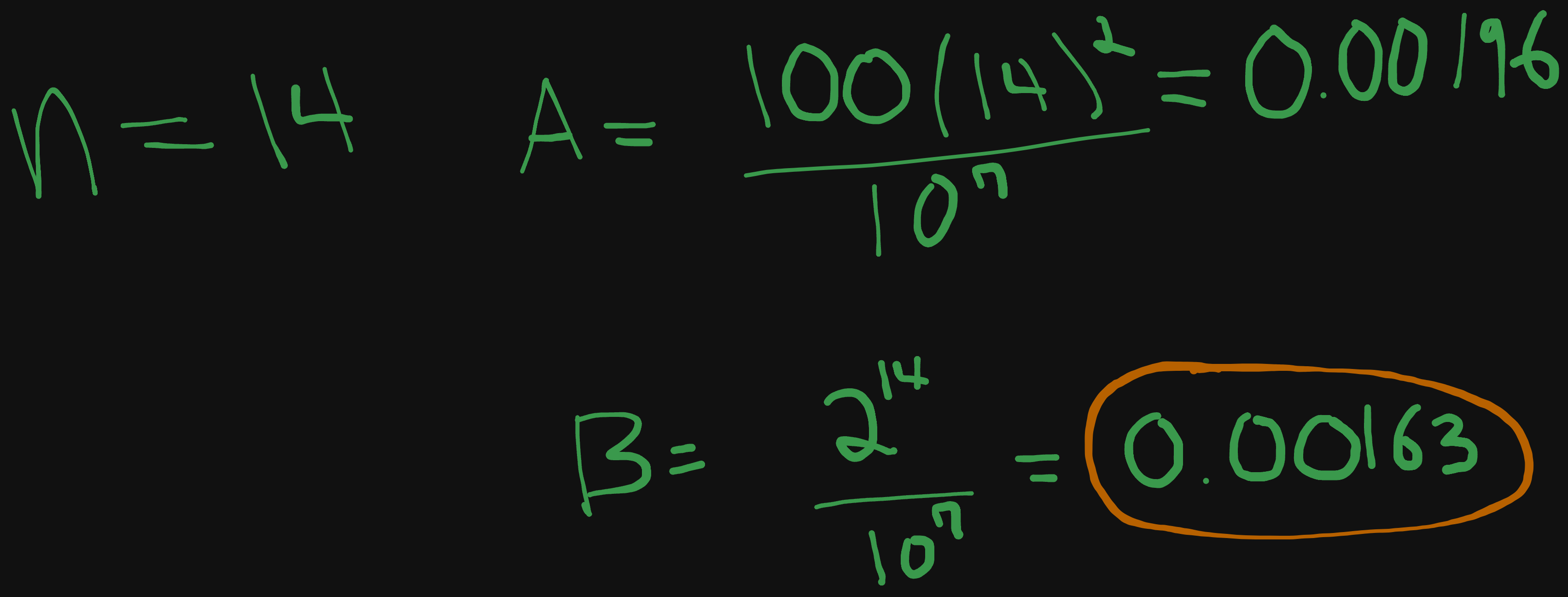
Yup, the next lowest has B winning. So the smallest value A can be is 15.

---

Next: Chapter 2