Grokking Algorithms - Chapter 8
Balanced Trees
From on out, if an array or linked list isn’t enough, a tree should be our next structure to try. It’s a balancing act to choose between both, especially for run time. Binary Search Trees are great, especially for insertion.
Remember, arrays take longer to insert than linked lists, but provide faster sorts. Binary Search Trees optimize by providing a clear and easy to understand structure: a root node with values larger to their right, and smaller to the left. This makes searches incredibly fast.
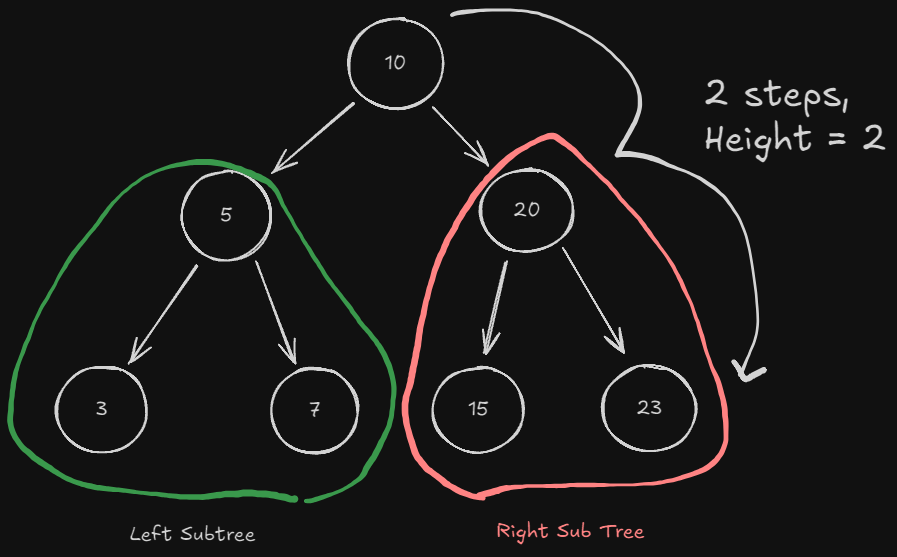
The height of your tree will determine the performance of it and algorithms performed on it. A bad scenario would be if all 6 nodes followed after one another. This would be unbalanced, which leads to our next subtype of tree. Before that, the runtime of the worst case for search would be $O(n)$ vs. the expected $O(\log n)$.
AVL Trees
To avoid the issue just presented, we have AVL Trees. They are a self-balancing tree, maintaining a runtime of $O(\log n)$. It maintains this using rotations. A difference of 1 is OK for height/balance, but anymore requires a rotation.
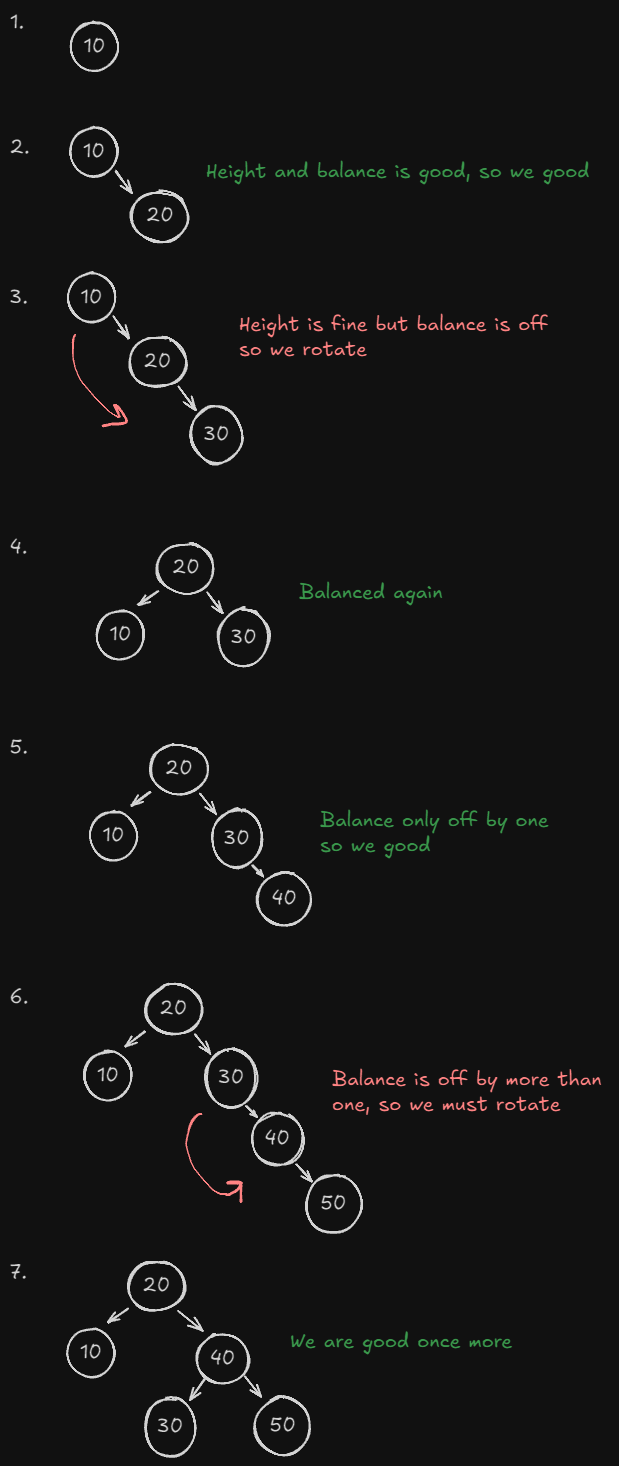
We visually can see when the balance is off, but we know this is purely our eyes doing the work for us. How does the structure know when the balance is off? Each node actually keeps track of two things; the height of the node and the balance factor of the node (-1, 0, or 1). If the balance factor is anything else, the tree knows when to rotate.

Our new Big O table for search & inserts looks more like this:
| Search | Insert | |
|---|---|---|
| Sorted Arrays | $O(\log n)$ | $O(n)$ |
| Linked Lists | $O(n)$ | $O(1)$ |
| Binary Search Trees | $O(\log n)$ | $O(\log n)$ |
Splay Trees
Another type of balanced BSTs, this time with a focus on speeding up lookups on commonly accesses elements. They do this by changing the root node to the most recently accessed each item on each retrieval. If the next search is for the most recently received item, the search is instant.
The only tradeoff here is that the tree is not guaranteed to be balanced. This is sometimes okay, but obviously depends on the situation.
B Trees
The last type of tree we are going to look at, B Trees are primarily used in database development. B Trees can have more than two children, and most importantly can have more than 1 key.
This multiple keys concept is important because of something called seek time. Essentially, it’s the physical time taken for your machine to literally read in data. B-trees save seek time by having larger read-ins, due to those nodes containing more than 1 key searches are more efficient.
Next: Chapter 9