Trees

A subset of graphs, trees are similarly made with nodes and edges and come in multiple different varieties. The first tree we are going to look at is the rooted tree, which is quite easy to visualize.

Rooted trees must have one node that heads to all other nodes in the tree. Nodes have at most one parent, and the only node with no parent is known as the root node. Nodes with no children are called leaf nodes.

File directories are a great example of a tree, and one in which we can run algorithms on.

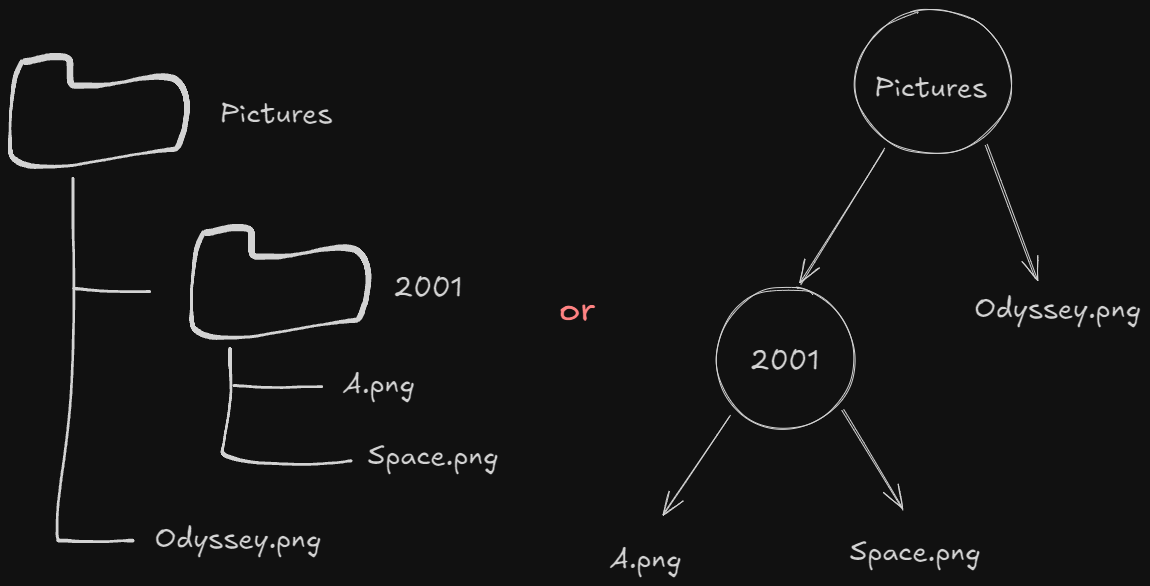
We could use BFS to get not only a target, but also list out all files as well:

from os import listdir
from os.path import isfile, join
from collections import deque

def print_names(start_dir):
	search_queue = deque()
	search_queue.append(start_dir)
	while search_queue:
		dir =  search_queue.popleft()
		for file in sorted(listdir(dir)):
			fullpath = join(dir, file)
			if isfile(fullpath):
				print(file)
			else:
				search_queue.append(fullpath)

This time around, we don’t have to keep track of the folders we go through, since there are no cycles in trees. If there is a cycle in your graph, it is not a tree, and you could run into infinite loops. Like many algorithms, we could also write this recursively, but it becomes a slightly different algorithm;

from os import listdir
from os.path import isfile, join

def print_names(dir):
	for file in sorted(listdir(dir)):
		fullpath = join(dir, file)
		if isfile(fullpath):
			print(file)
		else:
			print_names(fullpath)

The main difference here comes in how we reach our data and what we do when we get it, more specifically directories. In the first algorithm, we go through all the files in a directory no matter what, and store all directories found for later. In the second, if we come across a directory, we empty it immediately.

This second algorithm is actually called Depth-First Search. DFS cannot be used to find the shortest path however. This will change the way our print statement works:

# BFS print for the above example
odyssey.png
a.png
space.png

# DFS print 
a.png
space.png
odyssey.png

To provide a formal definition, trees are connected, acyclical graphs.

Binary Trees

Another common type of tree; nodes can only have at most two children: the left and right child (hence two). We’ll use binary trees a few times in the upcoming chapters.

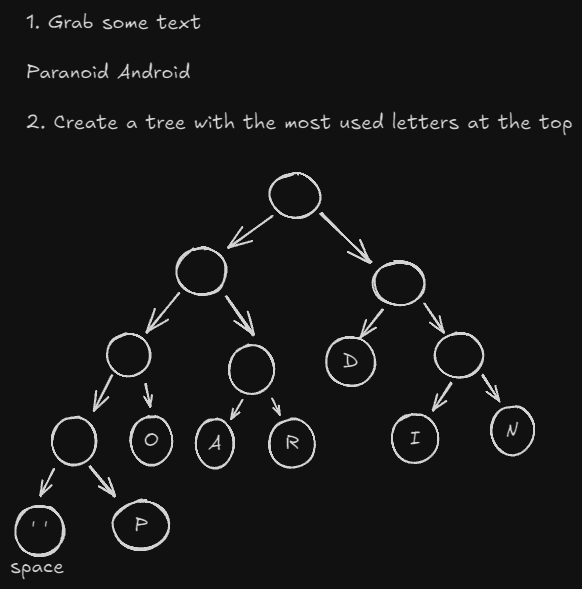
Huffman Coding uses binary trees to do character encoding. There is a larger lesson on encoding featured in this note. The biggest takeaway for now is that compression algorithms try to reduce the number of bits to store a character. Huffman looks at the characters being used and makes a binary tree with them to create text files using less than 8 bits. It doesn’t use standard chunking like bits and bytes, they can be any length.

Next: Chapter 8