Quicksort

Divide and Conquer

To introduce another tool into our algorithm toolbox, we can introduce Divide & Conquer, a useful method to recursively solve problems. Just like we learned in recursion, we need to identify our base case. Then we divide our problem into smaller problems, until we eventually reach our base case.

We can use the example of a plot of land:

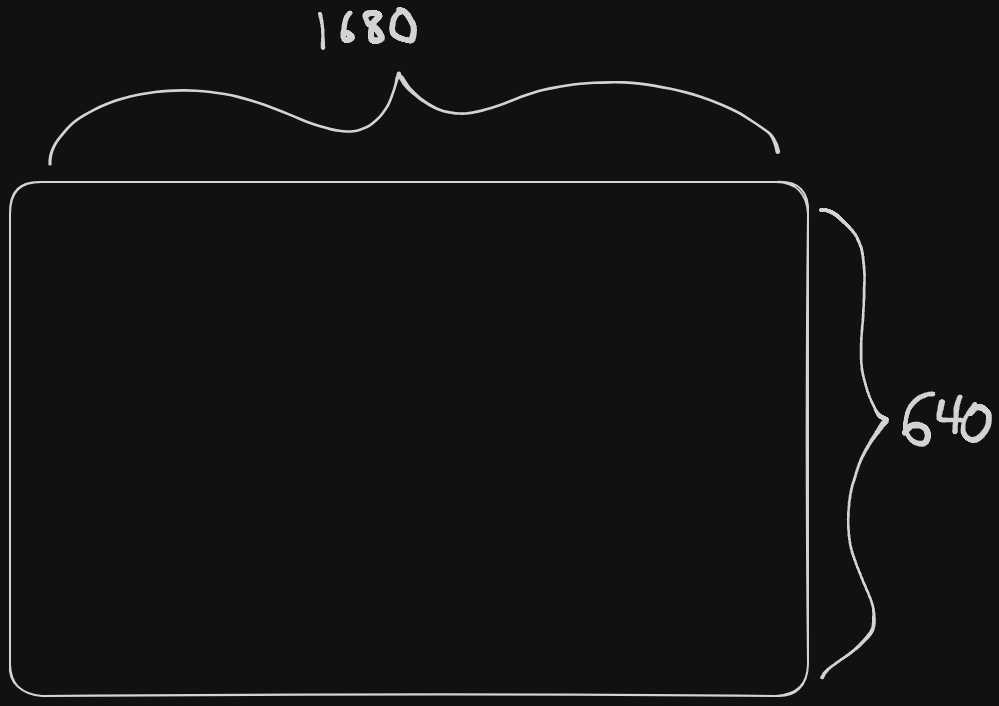
If we wanted to divide our land into perfectly even square boxes, making sure to use all available land with no land left out. How would you begin to figure this out?

In D&C’s case, we should determine a base case. A good way to think about this if one side is twice another, you could do a nice even split, so that’s our best case. If you try to make the most even boxes you can, this is what you end up with:

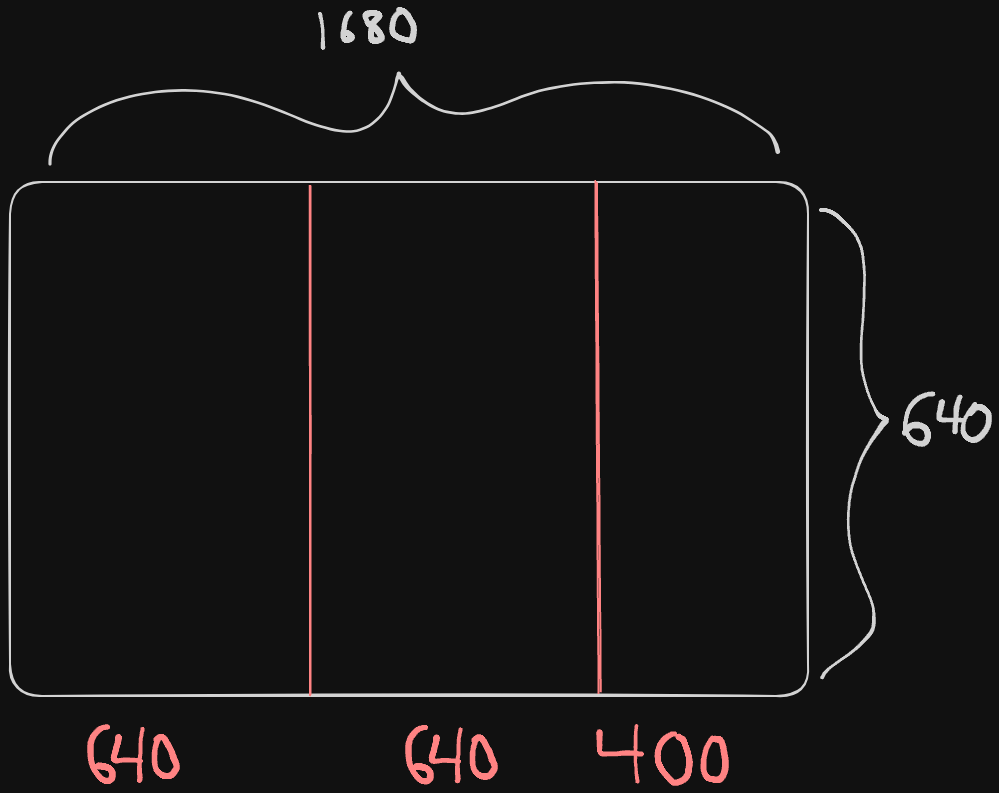
Thankfully, our recursive case is here to help us out. The same algorithm we used to D&C the first plot will be done to the remaining or leftover portion of land, in this case the 400x640 space. We continue to break down the portion until we are left with the an 80x160 portion, satisfying our best case and returning how large our square portions should be; 80x80!

D&C can also be used for finding things like sum and maximum. Recursive functions don’t rely or need variables; the stack is what keeps track of the values as you move through the recursive case.

Exercises

1. Write out the code for a recursive sum function

def sum_nums(nums):
	if nums == []:
		return 0
	return nums[0] + sum_nums(nums[1:])

2. Write out the code for a recursive counter

def count_nums(nums):
	if nums == []:
		return 0
	return 1 + count_nums(nums[1:])

3. Write a recursive function to find the max number in a list

def max_num(nums):
	if len(nums) == 2:
		return nums[0] if nums[0] > nums[1] else nums[1]
	sub_max = max_num(nums[1:])
	return nums[0] if nums[0] > sub_max else sub_max

1. For Binary Search, what is the best case and what is the recursive case?
   • Base Case: An array with 1 item: if it matches, great! If not, not in array
   • Recursive Case: Split the array in half, and search the remaining half

Quicksort

Obviously, quicksort is a sorting algorithm. It uses Divide & Conquer, hence when it was just introduced.

Right away, we identify our case case: arrays that don’t need to be sorted! An array with 0 or 1 element.

For a list of elements, to perform D&C, we have to choose a pivot point, or where we’ll split our array. For now, we can just choose the first number in the array.

After the pivot is found, we separate the remaining list into two categories, numbers smaller and larger than our pivot. This is known as partitioning.

Technically, this only works when the items before and after are sorted, correct? Well, that becomes our recursive case.

The code looks like this:

def quicksort(nums):  
    if len(nums) < 2:  
        return nums  
    else:  
        pivot = nums[0]  
        less = [i for i in nums[1:] if i <= pivot]  
        more = [i for i in nums[1:] if i > pivot]  
        return quicksort(less) + [pivot] + quicksort(more)  
  
  
print(quicksort([4, 1, 3 ,2, 8, 5]))

Revisiting Big O Notation

Quicksort is a unique algorithm due to it’s speed and times depending on your choice of pivot. Usually, constants don’t affect the run time, so we can ignore them. For quicksort, the average case is faster than quicksort even though they are both $O(n \log n)$.

In the worst case, the list is already sorted, and the pivot is the first number. You will have to move through the list of size $n$, $n$ times! Even in the worst situation, if you move the pivot to the middle, you make less recursive calls: $O(n)$ vs $O(\log n)$.

We touch all $n$ elements, every step of the way, taking $O(n)$ time. We have to account for that:

• Worst case, $O(n)$ with $O(n)$ steps = $O(n^2)$
• Best case, $O(\log n)$ with $O(n)$ steps = $O(n \log n)$

Quicksort is a fast sorting algorithm, and a great example of Divide & Conquer.

Exercises

How long in Big O for each?

1. Printing the value of each element in an array: $O(n)$
2. Doubling the value of each element: $O(n)$
3. Doubling the value of just the first element: $O(1)$
4. Creating a multiplication table with all the elements of an array: $O(n^2)$

Next: Chapter 5