Greedy Algorithms

A simpler concept than the last few we just tackled, Greedy Algorithms are algorithms that pick the most optimal movement at each step. This seems vague, and it is! You are literally just picking the most locally optimal solution, or the best choice, until you’re left with the globally optimal solution.

If you have a day where you’re trying to schedule classes & have as many as you possibly can, taking up your entire schedule. How would you plan your day? The major issue is that the classes times overlap; some start while others are still going, etc.

There are many ways we can try to solve this, but simplicity is sometimes all we need:

1. Pick the class that ends the soonest. This becomes your first class
2. Next, pick a class that starts after the first. This becomes your second class
3. Repeat until schedule is filled

In this situation, greedy algorithms helped out and made solving our problem extremely simple.

Here’s another scenario: We have a knapsack with a 35-pound weight limit. There are 3 items we can steal; A Nintendo Switch for $1500 weighing 15 pounds, a P.C. worth $3000 weighing 30 pounds, and Laptop for $2000 weighing 20 pounds.

In this situation, a greedy algorithm might actually hurt us more than help. A good greedy algorithm for this might be something like this;

1. Pick the most expensive item that fits
2. Pick the next most expensive item
3. Repeat until knapsack is full

This, unfortunately, would not give us desired results. If I went for the most expensive thing, I would have grabbed the P.C., and immediately filled up my bag. I have 5 pounds of wasted space. The better combination would have been to take the Switch and the Laptop, resulting in $5000 more.

Exercises

1. You work for a furniture moving company. Come up with a greedy algorithm to store the moving truck to maximize space. Will it give an optimal solution?

Store the largest box first, then store the next largest box, and repeat until the moving truck is full. This has the potential to be un-optimal, due to factors such as balance, # of items, size of items, etc.)

1. Say you’re traveling, and keep track of all the places you want to go with a number associated to show how much you want to go. Would a greedy algorithm work?

Yes it would work! Go to the attraction with the highest number, then the next highest, and so on. Even if you don’t get to do some things, you got the most important ones done first.

The Set Covering Problem

We’ve got an incredibly difficult task ahead of us; we want to start a radio show and want to reach all 50 states. We would have to map out all of the stations, since some overlap into similar areas.

To figure out the smallest set of stations to reach everyone, you actually have to list all possible subsets of stations (called a powerset). The time to run this is ($2^n$), which takes an extremely long time once you get past 10 stations.

Greedy algorithms can help us out here and help us get a good solution. More formally greedy algorithms are considered approximation algorithm, since the answer they return isn’t always the most optimal solution, it’s a good enough solution. The exact solution takes up too much time to figure out, so we can settle for good enough:

1. Pick the station that covers the most states not covered
2. Repeat until all states are covered

This will get us a fast, reasonably good answer that’s close to the optimal choice, and runs in $O(n^2)$! Much faster than before, and $n$ is the number of stations.

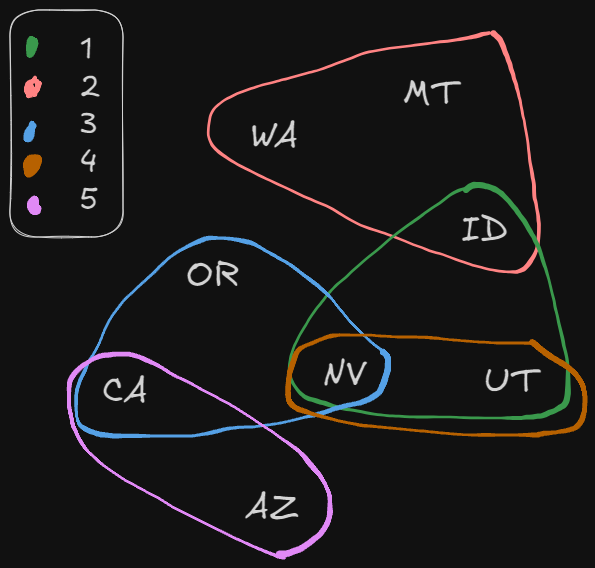
Instead of working with all 50 states, let’s just grab as subset of them, specifically the West Coast. The above diagram shows different stations, represented by different colors. The station numbers are noted in the key.

states_needed = set(['mt', 'wa','id', 'nv', 'ut', 'or', 'ca', 'az'])

stations = {}

stations['kone'] = set(['id', 'nv', 'ut'])
...

final_stations = set()

To actually calculate our answer, we need more variables. Our solution looks like this;

while states_needed:
	best_station = None
	states_covered = set()
	for station, states_for_station in station.items():
		covered = states_needed & states
		if len(covered) > len(states_covered):
			best_station = station
			states_covered = covered
	states_needed -= states_covered
	final_stations.add(best_station)

Next: Chapter 11