Introduction to Algorithms

An algorithm is simply a set of instructions or code designed in a way to accomplish a specific task. Tasks range from solving a math problem, to how to make decision given a specific scenario.

All the algorithms featured in this text are fast, solve interesting problems, or even both. The text will introduce an algorithm, give an example, and discuss the running time in Big O (we’ll get back to this in a second).

All algorithms can be found on their GitHub page, and one of the biggest themes of comparing them will be comparing their trade-offs, or the reasons to use an algorithm over the other.

Binary Search

Binary Search is a popular algorithm that takes a sorted list of values, and searches the list for a desired value, returning the value if found or NULL if not. To really get a sense of why we would use something like binary search, let’s compare it against simple search, where we check every element one at a time.

Let’s say we have a set of 200 numbers. If the number we need is in the last position, simple search would take 200 steps to reach the answer. Binary search however, splits the middle of the list, and eliminates half every time based on the feedback from the Algorithm. This is why the values must be sorted.

Using this example, we see that simple search takes $n$ steps, while binary search takes $\log n$ steps.

[!Math Lesson] So I had to go back and review Logarithms, which are actually just the inverse of exponents. See the drawing below to see what I mean. Also, all logs are going to base 2, so I’ll refrain from writing the 2 in the future.

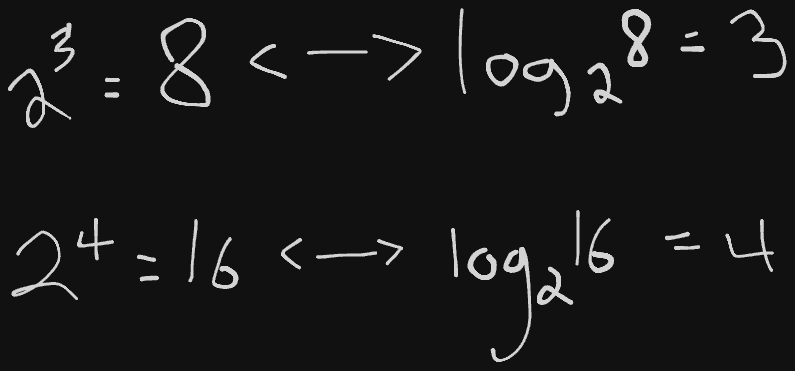
The Python code for this is actually quite readable:

def binary_search(nums, item):
    low = 0
    high = len(nums) - 1
	
	while low <= high:
	     middle = (low + high) // 2
	     guess = nums[middle]
	     if guess == item:
		     return middle
		 elif guess > item:
			 high = middle - 1
		 else:
			 low = middle + 1
	return None

A few important things to note here:

• We need to use the following to ensure there isn’t an out of range error:
  • High being set to len(nums) - 1
  • The while condition being low <= high
  • Using the guess variable instead of nums[middle]
• We don’t need another elif, since we already check for two of the three possibilities

Exercises

1. Suppose you have a sorted list of 128 names, and you’re searching using Binary search. What is the max number of steps?
   • 7
2. What if we doubled the size of the list?
   • Only one more step! 8

Running Time

When discussing algorithms, we’re often mostly concerned with the running time, or how long it takes to complete the task of said algorithm. The most common way to represent this is with Big O Notation. Big “O” is an unique operator used to represent any algorithms run-time (specifically the worst-case, but we’ll come back to that later).

Different algorithms grow at different rates; if they didn’t, there would be no real need to use one algorithm over another. Let’s compare the rates of simple search vs. binary search:

• If one operation takes 1 millisecond, it would take a billion milliseconds to search through a billion-length list, vs. binary sort which takes around 30 milliseconds
  • They clearly do not grow at the same rate

Big O helps us compare the number of operations done in an algorithm. Specifically, this notation describes the worst case, or how many operations will have to occur in the worst-case scenario. Like in the example above, simple search for a billion-length list takes a billion steps, meaning O(1000000). We simplify it with a placeholder, usually $n$.

Here is a list of common Big O times from fastest to longest:

• $O(\log n)$
• $O(n)$
• $O(n*\log n)$
• $O(n^2)$
• $O(n!)$

If we took these five times and visualized how fast they grew, it would look something like this;

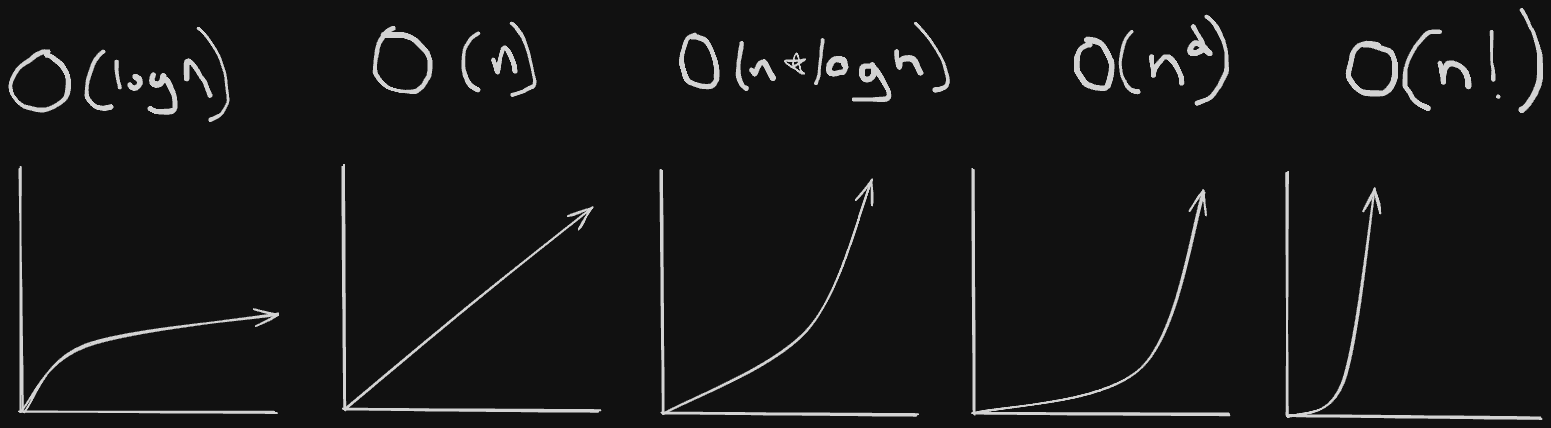
A key thing to remember is that an algorithm’s speed is not measured with time, but with operation steps or actions taken. We refer to how quick an algorithm is by how it scales as the input increases.

Exercises

3. You have a name, and want to find the person’s phone number in a phone book. What would be our worst-case runtime in Big O notation?
   • $O(\log n)$
4. You have a phone number, and want to find the person’s name.
   • $O(n)$
5. You want to read the number of every person in the phone book.
   • $O(n)$
6. You want to read the numbers of just the “A"s
   • $O(n)$

The Traveling Salesperson

One of the most infamous problems in Computer Science, and a great example of how terrifying scaling can actually be, is the issue of the traveling salesperson.

Imagine you are a salesperson, and your goal is to travel to 5 different cities to sell your product. Naturally, you’re going to want to take your time to decide on what route you should take. Well, for only 5 cities, if you wanted to go over all of the possible routes you could take, you would go through 120 different permutations. Not that many, right?

Well, let’s throw in another city. Now, you have to account for 720 permutations. A huge jump up. A step or two further, how about 8 cities? 40,320 permutations. This is pretty abysmal. If you wanted to for example, try to even think about over 100 cities, it would take longer than the sun has left to live before you’d reach that conclusion.

We consider the runtime for this problem $O(n!)$, and many believe there is no way for the outcome to improve.

Next: Chapter 2