Unit 1: Digital Information

Most of this I should know, being a computer science teacher. However, outlining this should make teaching this rather boring portion easier. I want to try implementing more diagrams while I teach; I’ll be looking forward to stealing their ideas.

Bits and bytes

How do computers represent data?

All computers understand is Binary, 0’s and 1’s.

The video explains the example of using one single wire to transfer electricity through it; on or off. This is the most fundamental understanding of how our computers function. This is just one single bit. Common machines use hundreds of thousands of bits to achieve their objective.

With text, it’s easier to visualize. Every character has a value related to some makeup of a 0 and a 1. Images are harder, since they’re made up of tiny pixels. Each pixel holds a color. Each color can thankfully be represented by a number. Think about videos, that are rendering 30 to 60 images per second.

Audio can also be broken down into numbers, usually by vibrations as a waveform, and that waveform as a number.

Bits hold only a single value, on or off. Generally only binary decisions are used by single bits.

Computers will use multiple bits to represent more complex data. The more bits, the more information deliverable.

We can see that a sequence of two bits can represent four (2^2) distinct values:

00, 01, 10, 11

While a sequence of three bits can represent eight (2^3) distinct values:

000, 001, 010, 011, 100, 101, 110, 111

While a bit is a single piece of information, a byte is a unit that consists of 8 bits.

The conversion is pretty simple: multiple by 8 to go from bits to bytes, and divide by 8 to go from bytes to bits.

Binary Numbers

The binary number system works very similarly to how decimal numbers work.

In decimal numbers, you multiply each number by a different power of 10. You start in the ones’ place, the tens’ place, and the hundreds’ place. 234 is equal to (2 * 100) + (3 * 10) + (4 * 1). Ones’ place is 10^0, tens’ place is 10^1, and hundreds’ place is 10^2.

The binary number system multiplies to the power of 2 instead of 10.

The decimal number 1, can be represented in binary as 0001. That’s the same as (0 * 8) + (0 * 4) + (0 * 2) + (1 * 1), or 0 + 0 + 0 + 1, which gives you 1.

The decimal number 10, in binary is 1010. We know this because of (1 * 8) + (0 * 4) + (1 * 2) + (0 * 1), which is 8 + 0 + 2 + 0, which equals 10.

Converting decimal to binary

Limitations of Storing Numbers

Number limits, overflow, and roundoff

Storing numbers requires some work for binary representation. We run into issues with problems like roundoff, overflow, and precision. These issues are usually centered around memory issues.

Integer representation

An integer is any whole number: 1, 10, 230, -400 are all integers. In order to store integers, for however many bits the number is stored in, the first indicates the sign, and the others contain the absolute value.

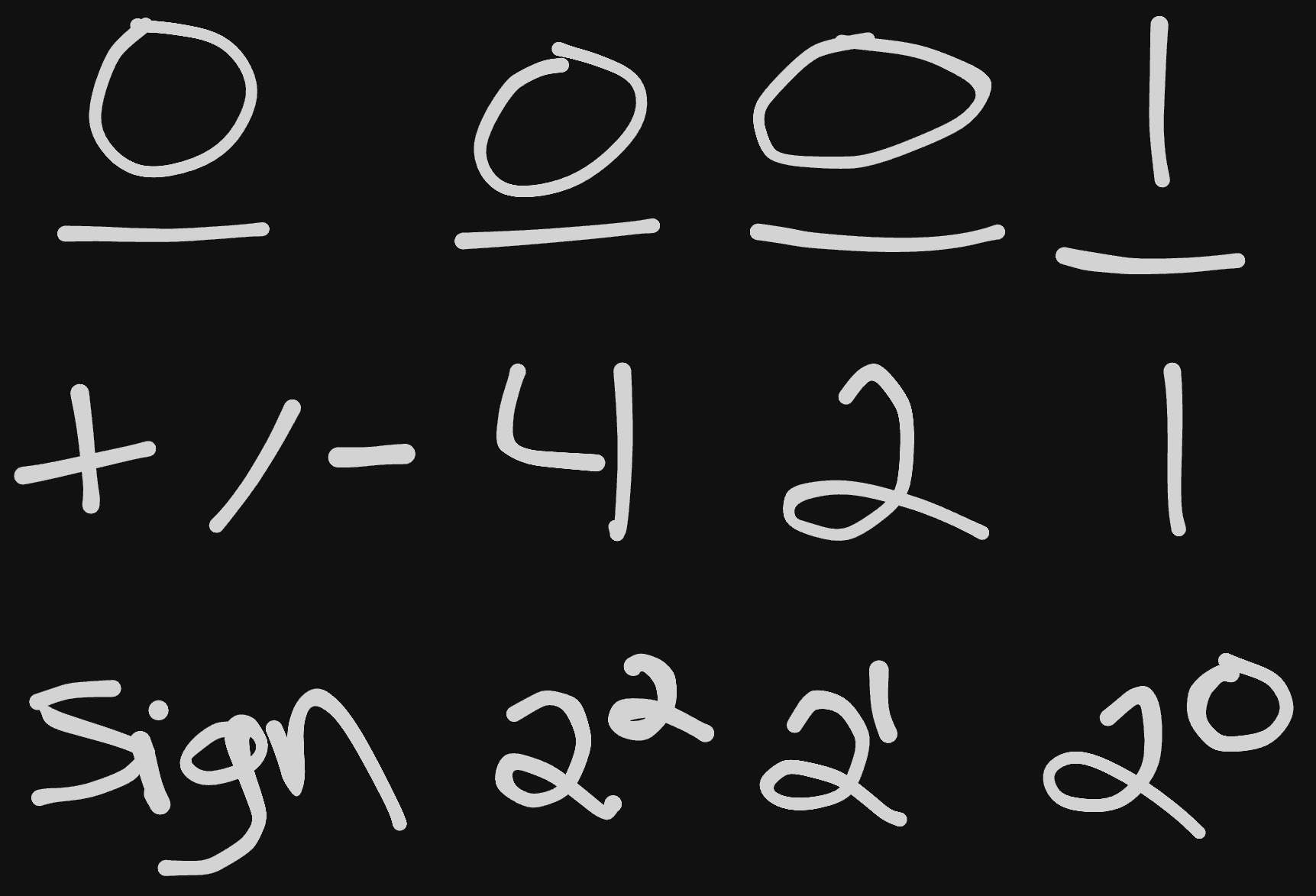
Overflow

Let’s suggest we only have 4-bits of memory to store our integers on a computer. That means we could only store up to the number 7. If we were to then try to go beyond it, like say with the following code:

x = 7
y = x + 1

x is easily able to be stored, but y would give us a problem since it goes beyond the capabilities of our systems memory. This type of error is called an Overflow Error. Some systems might throw this error, truncate it to 7, or wrap back to 1.

Thankfully, 64-bit is the common standard.

Floating-point representation

Floating-point numbers represent every number that isn’t an integer-irrational, fractional, etc.

In floating-point representation, a number is multiplied by a base that’s raised to some exponent.

In mathematics it often looks like this: 300=3*10^2

Since computers use the binary system instead of the decimal system, it looks like this: 128=1*2^7.

Numbers between the powers of 2 end up looking more so like this: 160=1.25*2^7, or 0.25=1*2^-2.

Modern 64 bit systems use 1 bit for the sign, 11 bits for the exponent, and 52 bits for the number in the front.

Roundoff errors

There are still some issues since there are some numbers that can’t be easily represented. .3^- (repeating) is an infinitely repeating sequence that can’t be stored in any device. The computer will eventually have to round at some point. A roundoff error is when we get an unexpected error due to the computers rounding of a complicated-to-represent number.

8/10/2024

Storing Text in Binary

Obviously, computers can do more than just store numbers. For example, we often use emojis. These icons, or symbols, are agreed upon and referenced under an encoding system.

Encoding systems all have names to make it easier to discern what they’re used for. If we assign a peace sign to the value 10, and and heart to the value 01, we could say 0110 would be a heart then a peace sign. But, the computer just has to store the values, instead of having to find a way to store those icons in binary.

ASCII Encoding is a common encoding standard that is still used today. It’s encoded using 7-bit binary, meaning it can only have 128 permutations. Many of the codes are for actions, like line return or space. While the letters have both upper and lowercase variations, as well as numbers.

ASCII’s problems stem from it’s lack of scalability. ASCII can only account for words written in plain English: any accent marks or foreign letters won’t work. Same goes for any Chinese or Japanese kanji.

Since ASCII is also 7-bit, and Computers store things in parts of 8-bits, there’s a small waste of memory.

To solve these problems and make computers more accessible, programmers started with Unicode. Unicode is a character set that has a code point (stored in hexadecimal) for each of the world’s language-characters. Currently, Unicode has over 130,000 characters represented.

The encoding system used alongside Unicode is UTF-8, that works with both ASCII and Unicode. UTF-8 has the ability to represent any Unicode character using ASCII code, while only using 1 to 4 bytes.

UTF-8 works pretty interestingly to define how many bytes are used with it’s binary representation: if there are no 1’s in the prefix, that means the character a single byte and can be represented using ASCII. If there are two 1’s, there are two bytes, 3 1’s means three bytes, and so on to four.

Converting Analog Data to Binary

The real doesn’t work in binary; it moves too fast and constant. This data is called Analog data.

It’s far too complicated to just take in and display, but we can do a few steps in order to get there. Let’s start with a basic analog signal.

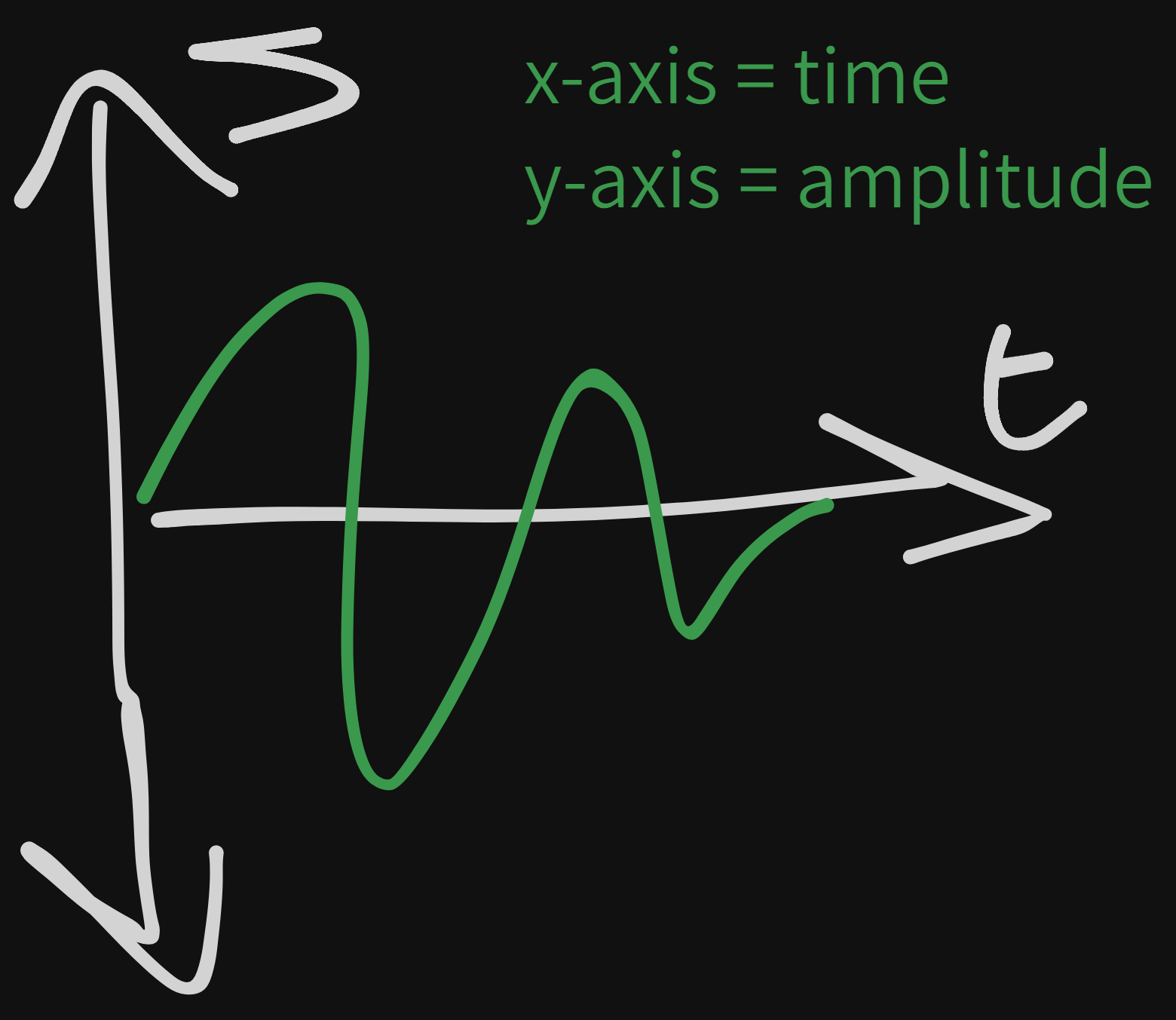
We could grab a random point on the green line and define the analog information in terms of seconds long or volts used.

Sampling is the process of selecting points after a desired interval (every 1 second, every 30 milliseconds, etc.). If we were to grab a point from the above graph every 30 milliseconds:

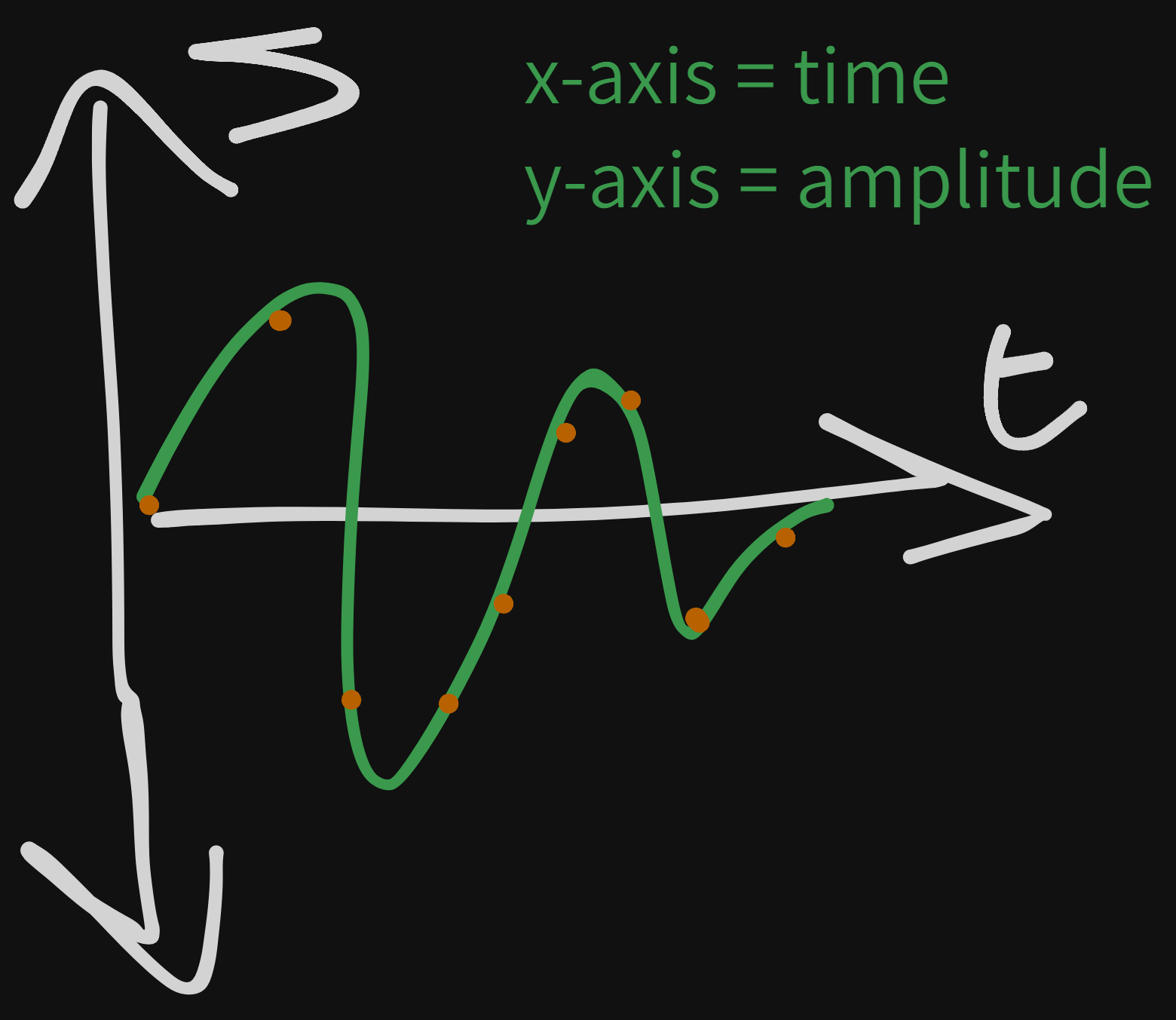
Each orange point would become a (x, y) coordinate. It could play these 9 orange points, and depending on the complexity of the sound, it could either be or not be enough to accurately display it.

We call the sampling rate the number of samples taken in some unit of time. Given the above example, with a sampling interval of 30 milliseconds, it would take 33.33 samples per second.

We can quantify a sufficient sampling rate by saying that the rate should be larger or equal to twice the highest frequency in said signal. This is where we get hertz from; frequency can be defined as the number of cycles per second, which get measured in Hz.

If we say, have a signal with a max of 250 Hz, we should use a sampling rate of at least 500 Hz. The sampling rate for music is commonly 48 kHz.

Since noise is constant and difficult to quantify still, we need to incorporate Quantization. Using our example from above, we can break it down to say that our signal has a range of about -100 to 100 volts. To make things simple, we can easily use intervals of 25 volts to take in data more uniformly:

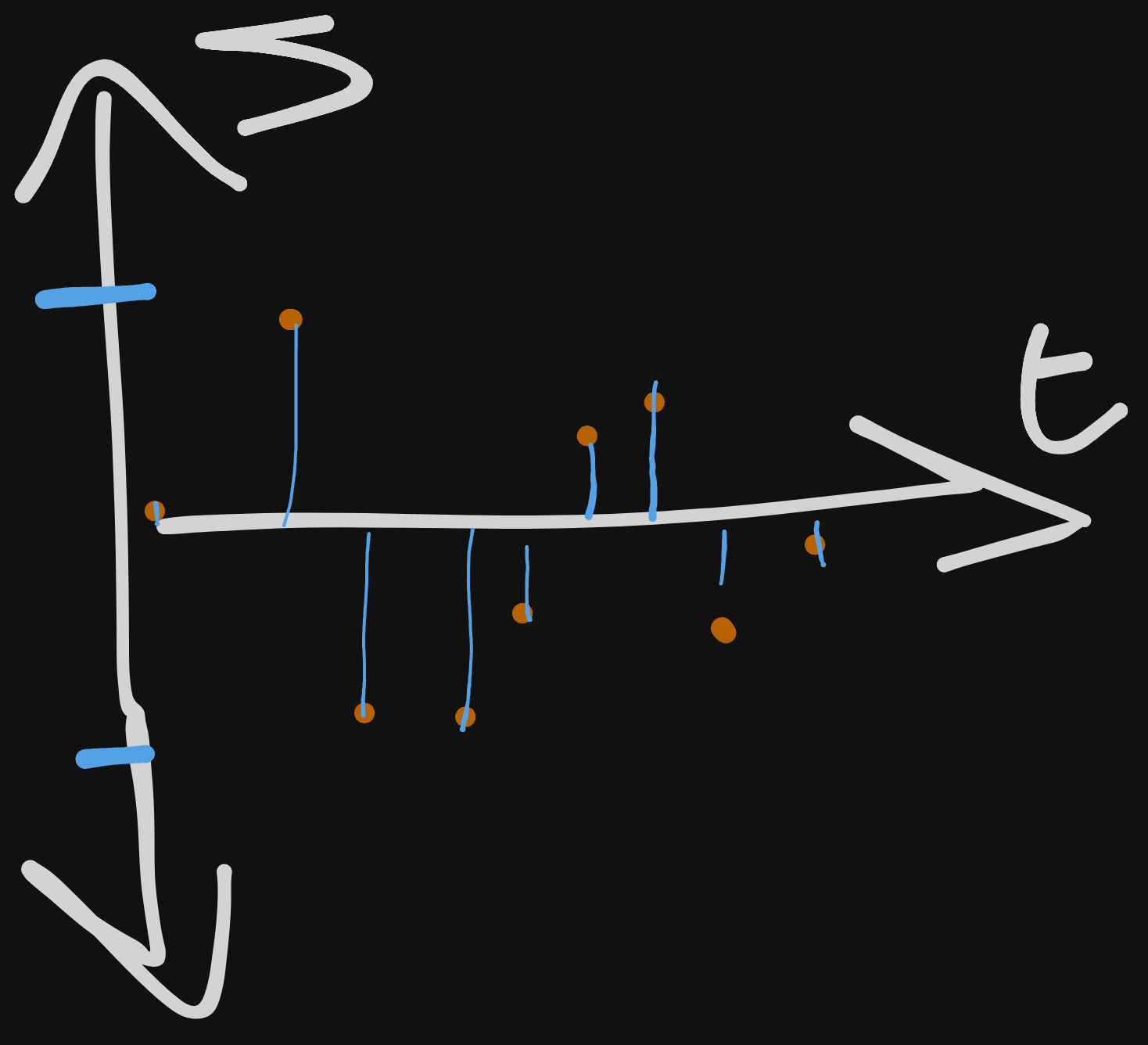
The blue points are our nicely formatted coordinates; they may not be exact, but they’ll approximate.

The last part of our encoding process is binary encoding. In situations where there aren’t many quantized y-values, the computer does not need to store the actual value. These values get stored as a binary sequence.

For a computer to understand that binary sequence, it also needs to have information on how it was sampled and encoded. We can use bit depth to represent bits per sample.

Telephone calls have a bit depth of 8 bits (256 values) while YouTube music videos is 24 bits (over 16 million values).

After all of these steps, we put them back together in a process called Reconstruction. The reconstruction will look very close to the original, but will mess some specific things up.

8/14/2024

Lossless Data Compression

Since everyone uses data, and data storage isn’t free, we have to be conscious about the amount of data we are using when storing our documents, images, videos, etc. In order to make the collection of all of these formats easier, the concept of compression was implemented.

To compress something is to reduce the amount of storage needed for a file. Depending on the file’s type, different methods of compression exist.

Lossless compression algorithms are for when the information contained in the document is important enough so that when we reduce the size it doesn’t take away any quality from the original file. Think of your word documents; how bad would it be to lose the third word in every sentence for the first 10 pages? Pretty detrimental.

Lossy compression algorithms on the other hand reduce the size of the file with less care; the file size being reduced a great amount is more important than what is in the file. When you for example compress an image, often the image will lose that term we call “sharpness” to the original image.

Lossless Text Compression

Lossless text compression algorithms work similarly to how English text slang works. Shortening phrases like lol, ggwp, gitgud, and so on, take full English phrases and symbolize the full words. We recognize them (though I doubt a Victorian child would know what those words mean) and understand their meaning.

Text compression will find repeatable phrases that occur often and will replace them with some symbol. If “the” appears 10,000 times in a document, likely it will be replaced with some representative symbol and translated back when sized back up for modifying.

Lossless Image Compression

Slightly more complicated than text, but the concepts are similar. Before we dive in, let’s explore how some basic images can be represented, aka bitmaps.

As we should already know, images on screens are just pixels, every single image contains a color on the RGB scale. Bitmaps are images that can displayed with binary pixels, of 0 and 1. Some know this style as pixel art. Usually it’s black and white, but the system can work with any two colors.

Now if we were to look at really basic example of a heart:

0001100000110000
0011110001111000
0111111011111100
1111111111111110
1111111111111110
1111111111111110
1111111111111110
1111111111111110
0111111111111100
0011111111111000
0001111111110000
0000111111100000
0000011111000000
0000001110000000
0000000100000000

It’s a little hard to see but I promise, that’s a heart. If we weren’t sitting at nice computers and you wanted to describe this image to me so I could draw it in bitmap style, you probably would get tired of saying each number individually. You might start to tell me how many of each there are to save me time, like for example with row 3, “one 0, six 1s, one 0, six 1s, two 0s” all the way down and it would probably save your voice some unnecessary strain.

Computers can use an algorithm called RLE compression that has a similar logic. Run-length encoding will replace a row with the first number of white pixels, then red, then white, and so on until the row is finished. The third row which is 0111111011111100 would become 1,6,1,6,2.

Funnily enough, since RLE always starts with the white pixel, a row like 4, 1111111111111110, would be written as 0,15,1.

Since it has this “map” of every pixel, a perfect representation from decompression is possible.

Compression Ratio

If we were to continuously make our image of a heart larger (ours is 16x16), the RLE algorithm would increasingly save us more time. It works so nicely because our heart has a lot of fill for one color; black (or red, or whatever). It can easily reduce the amount of pixels into one color, since there is so much fill without breaks or details.

If we had more complicated images, say a crown or a lion, it would have so much detail the compression wouldn’t save nearly as much space as the simple heart would. Regardless, space would be saved, and the image would lose 0 detail upon decompression.

Limits of RLE

RLE’s use-case really ends once you leave perfectly representable images. Images that have a different color for every pixel wouldn’t even be able to use RLE; there are no “runs” to be made! Regardless of how big or small the image is, there is no way to represent a complex image with 0s and 1s without massive quality loss. Sometimes though, that can be a look, so always experiment and have fun with it.

RLE is used today, but mainly in Fax machines, where black and white are the only options.

Lossy Compression

Now that we understand Lossless, let’s examine lossy more closely. Like we defined earlier, there are certain files that don’t need exact 1 to 1 representation. Often these files are large enough that a small trim off the top will barely be noticeable.

Matter of fact, if I were to compress an image, most if not all people would not be able to tell the difference between the two.

For images, lossy compression algorithms can do something rather interesting; they use brightness version of an image (just black and white) and doing a procedure called chroma subsampling. The chroma version of the image, or color version, is searched through for similar color values, then approximates them based on some average (usually some multiple of 2) to transform nearby pixels into one uniform color.

For audio, because the limits of the human ear are well understood, there are aspects of sound that we never hear. When audio files are compressed, these inaudible sections of the file are dropped and not missed.

Lossless vs. Lossy

Choosing between the two comes down to the objective and limitations of your project. Most things these days will end up using some lossy algorithm, but when they do we often have a choice of how much we want to retain. You can look no further than any image or video editing software out there; when finishing up any project and exporting, it will ask for quality, usually in a percentage format. The higher the quality, the more space it’ll take.

Digital Copyright

I was hesitant to go deeper into this, since it’s not necessarily a topic I’m interested in, but I should get the definitions down just to be safe.

How copyright works in the states:

Authors are able to copyright their creative ideas. Once published, Authors automatically have claim to their copyright, but should in order for Court proceedings.

Authors have the right too:

• Reproduce their own work
• Create derivative works
• Distribute copies via sale/rental
• Publicly display visuals/perform audio works using said material

Copyrights usually end ~70 years after the authors death, and enters the public domain.

The term fair use is related to the act of using some copyrighted material, that isn’t infringing on any of the rights that we listed up above. Often if for something small, non-profit, and local, can we use things like copyrighted material. Once we enter the profit sphere, or get larger using other people’s material, do we break fair use.

DRM and DMCA

Digital Rights Management, or DRM, is the security providers will put on their digital media in order to prevent the breaking of fair use laws. For example, for e-readers like the Kindle, Amazon might but DRM on their eBook files that don’t allow for non-kindle devices to be able to read their files; it would actually encrypt the file unless used through a Amazon device.

Another example is Music; Spotify will use DRM on their sound files, so that if pirated and ripped onto a non-Spotify player, the audio will end up corrupted and non-playable.

DMCA, or the Digital Millennium Copyright Act, is used almost more as a verb today than known as the act. When someone is using copyrighted material, the person who owns the property could flag that person for using their material without permission, taking down whatever use case the situation started in. Streaming on Twitch and you used non-public domain music? You could get flagged, and the video could get taken down, which we would say, “The VOD got DMCA’d”.

Creative Commons and Open Source

In order to streamline the process of Copyrighting online content, Creative Commons came about. CC offers licenses for sharing and how to use said online material. If material does have a CC it is usually displayed somewhere near the content, and can be searched and filtered relatively easily.

Open Source is a concept that says the material used to write the content (usually some code base) is free and available to use in order to make writing software more compatible and alike. Even some licenses can be open source- the MIT license allows you to label your code under it’s umbrella, allowing for applications to be rapidly created and released.

Next: Unit 2